
當我們將肌電訊號轉換成頻譜(Power spectrum)後,我們的確可
以看到頻率和其強度的分佈,不過這代表什麼意義呢?
我們知道我們的肌肉由不同型態組成,簡單的說可以分為快肌
(fast twitch)跟慢肌(slow twitch),快肌肌肉纖維較粗,動作速
度快,不過較容易疲勞,慢肌動作速度慢,但是可以作用持續時間長,
就傳遞肌肉表面膜電位而言,快肌就像比較粗的電線,傳遞訊號的速度
較快,因此由電極片所接收到單位時間內的電位差訊號相對而言就會比
較多,所以頻率會落在比較高的位置,反觀慢肌,則為相反地現象。

而我們的肌肉,則由不同比例的快慢肌所組成,例如我們強而有力
的肱二頭肌(biceps),快肌的組成較多,所以也比較容易酸。
不過因為頻譜看出來的是各個頻率強度的變化,如果要相互比較的
話,則必須要像一個常態分佈圖形一樣,有平均數(mean),等數值,
比較常用來作為計算的為中位頻率(Median frequency)。
中位頻率(Median frequency),其定義為頻譜分析圖中,將其強
度由低頻積分到高頻,積分面積為全部面積一半時的頻率。因此就可以
中位頻率來作為訓練或是疲勞測試後,改變肌肉組成比例(訓練)或是
影響肌肉放電(疲勞)等改變觀察。

因此利用傅立葉轉換以及if指令來求得中位頻率,當積分到某一點
時,大於全部等積分的一半時的頻率即是中位頻率。
由於肌電訊號是時間性的,我們比較常做的方式會像之前所用的以
window的方式,每多少點計算一次,重複多少點,然而取樣頻率
(sampling rate)會影響最後每一個點所代表的頻率,所以也必須考慮
。
function [med_fq]=fft_i(data,n,op,sr)
% fft for n point
% op: the point of overlapping
% med_fq is the median frequency of the power spectrum
% sr is the sampling frequency
% calculate the times of the loop (-1 due to the initial loop is 0)
l=fix(length(data)/op-1);
fq=(1:n/2).*sr/n; % calculate the frequency of each point
for i = 0:(l-1)
int=1+op*i; % the initial value of the loop
f=fft(data(int:(int+511))); % fft for the data
mag=abs(f); % Amplitude of the fft
mag=mag(1:n/2);
for k=1:n/2
if sum(mag(1:k)) >= sum(mag)/2
med=k;
break
end
end
med_fq(i+1,1)=k*sr/n;
end
% calculate the final part of the sample
int=1+op*l;
f=fft(data(int:end)); % fft for the data
mag=abs(f); % Amplitude of the fft
mag=mag(1:n/2);
for k=1:n/2
if sum(mag(1:k)) >= sum(mag)/2
med=k;
break
end
end
med_fq(l+1,1)=k*sr/n;
首先必須先計算迴圈的次數,以所有的點數除上重複的點數(通常
會以window點數的一半)減一(種樹法則),然後就每多少點作一次傅
立葉轉換並且求得中位頻率,值得注意的是,因為常常所選取的資料數
並不能剛好夠最後一筆,舉例而言,也就是說原本應該要以512個點作計
算,但是迴圈到最後一次時可能只剩下500點,由於fft這個函數當不夠
點的時候會比剩下的點以零帶入,所以最後一個窗口則以另外方式計算
。
執行結果
>> data=textread('D:/EMG_fft.txt');
>> plot(data);
>> med_fq=fft_i(data,512,256,1000);
>> figure(2);plot(med_fq)

這是原始資料圖,資料可以
由此下載 經由計算後為

一開始很高可能是因為在還沒有任何訊號時就已經存在的高頻雜訊,
此時就要利用之前提得濾波器給予濾波。

肌電訊號分析可以分為兩個主要部份,一個即是時域
(time domain)另一則是頻域(frequency domain)。
大部分例如方均根植(root mean square)或是找尋
起始點(onset point),是屬於時域的部份;然而頻域的
部份會著重去看頻率和強度之間的關係(power spectrum)
,而以下所介紹的為利用傅立葉轉換(Fourier transform)
所做出的關係圖。
程式如下
data=textread('D:\EMG.txt');
fft_data=fft(data);
mag=abs(fft_data);
fq=(1:length(data)/2).*1200/length(data); % 每一點的所表示的頻率
mag=mag(1:length(data)/2); % 因為另一半為image
plot(fq,mag)
首先可以發現到當對傅立葉轉換後的圖形如下,每個
點都是有相位與長度大小的點。所做出為複數座標系的圖
。
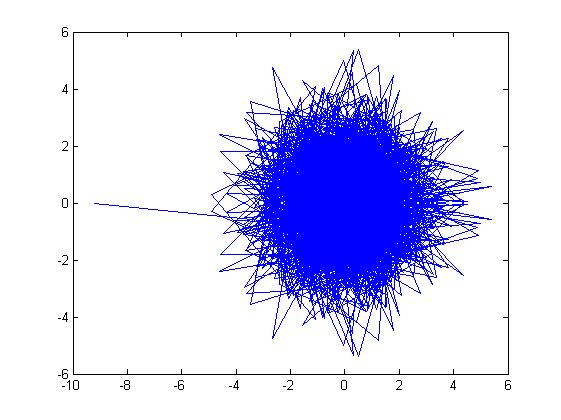
不過對於分析強度和頻率而言,只要去看轉換後每個
點的強度即可,所以將傅立葉轉換後的值取絕對值,即是
強度。
作圖後可以發現到,會是一個以中線分隔兩邊成左右
對稱的圖形也表示只有在一半以下的點是有意義的。
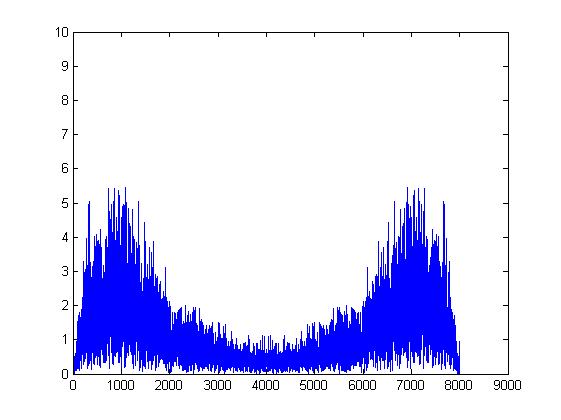
至於為什麼只有一半是有意義而另一半會是跟前一半
對稱鏡射,這是由於我們取樣頻率的關係。
正確的取樣頻率必須至少是原來訊號的兩倍,這就是
所謂的Nyquist rate。即是Nyquist Theorem。
由下圖可以見到,如果取樣頻率較小,原始訊號頻率
很高,所取的訊號圖形和原始訊號就有差距,而變成較低
頻的訊號。

而每一個點所代表的頻率則為”取樣頻率/點數”,
由於只有一半的值是有意義的,所以須將頻率以及強度作
處理,如下:
fq=(1:length(data)/2).*1200/length(data); % 每一點的所表示的頻率
mag=mag(1:length(data)/2); % 因為另一半為image
因此做出來的圖形如下
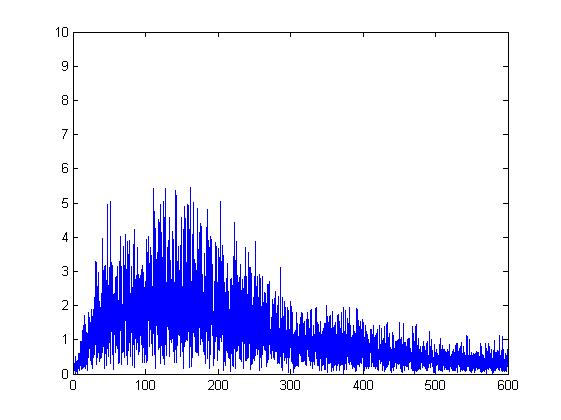

一般我們在分析肌電訊號的時候簡單方式,讓訊號有如封包(envelope)一樣,或是利用這些方式作為分析比較。
常用的有,一階的低通濾波,方均根(rootmean square),或是平均的方式以及積分的方式。然而由於取樣頻率高,因此我們不可能把所選取的範圍全部一次作處理,而會利用窗(window)的方式,其意義是,每次選取特定的點作處理。
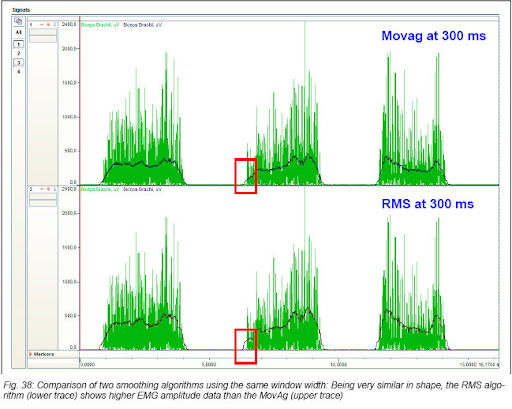
依據這樣的概念,利用for loop的方式,也就是每次選取固定的點作為分析使用。
舉例而言,下圖是一段EMG的訊號。
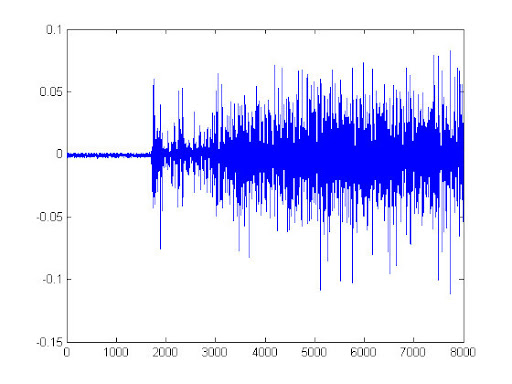
以下是所撰寫的程式碼
function [out point]=moving_avg(data,dur)
l=length(data);
k=menu('Select the function','Average','RMS');
switch k
case 1
for i=1:(length(data)-dur);
out(i,1)=mean(abs(data(i:i+dur,1)));
point(i,1)=(i+i+dur)/2;
end
case 2
for i=1:(length(data)-dur);
out(i,1)=sqrt(sum(data(i:i+dur,1).^2)/dur);
point(i,1)=(i+i+dur)/2;
end
end
使用的情形如下
目前以menu方式寫成兩種處理方式。point是說明每一次作處理後點應該落的位置(因為10作完後只有一個點)。
其結果和原始訊號圖畫在一起如下
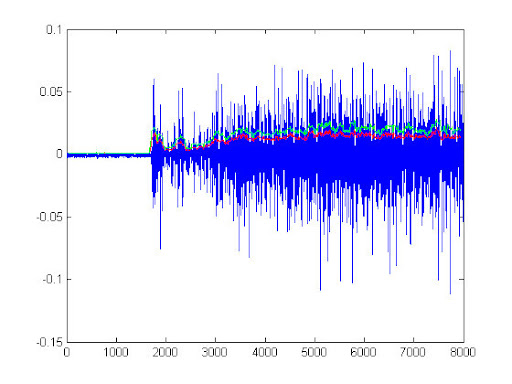
管路中之損失除管路本身外,其出口、入口及管徑擴張之損失均與動能有關,即V
2/(2g)之係數。其程式內容如下
% pipefittings.m
% Local losses at pipe fittings
%
while 1
k=menu('請輸入接合件之型式','驟然放大','驟然逸出','擴 大 管');
Q=input('請輸入管路流量(m^3/s)[10]: ','s');
if isempty(Q), Q='10';end
D1=input('請輸入入口管徑(m)[1]: ','s');
if isempty(D1), D1='1';end
d1=str2num(D1);
ke=str2num(Q)./(pi*d1.^2/4)/(2*9.81);
switch k
case 1
HL=ke;
case 2
HL=ke/2;
case 3
D2=input('請輸入出口管徑(m)[2]: ','s');
if isempty(D2), D2='2';end
HL=(1-(d1./str2num(D2)).^2).*ke;
end
disp(['此接頭損失為 ' num2str(HL) ' (m).'])
A=input('是否繼續執行(Y/N)[Y]:','s');
if isempty(A), A='Y';end
if upper(A)~='Y', break;end
disp('請由選單選擇轉換單位。。。')
end
管路配件損頭經過認養後
% pipefittings.m
% Local losses at pipe fittings
%
while 1
k=menu('請輸入接合件之型式','驟然放大','驟然逸出','擴 大 管');
switch k
case 1
prompt = {'請輸入管路流量(m^3/s)[10]','請輸入入口管徑(m)[1]:'};
dlg_title = '您所選擇的是驟然放大';
num_lines = 1;
def = {'10','1'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
Q=answer{1,1};d1=answer{2,1};
ke=Q./(pi*d1.^2/4)/(2*9.81);
HL=ke;
case 2
prompt = {'請輸入管路流量(m^3/s)[10]','請輸入入口管徑(m)[1]:'};
dlg_title = '您所選擇的是驟然逸出';
num_lines = 1;
def = {'10','1'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
Q=answer{1,1};d1=answer{2,1};
ke=Q./(pi*d1.^2/4)/(2*9.81);
HL=ke/2;
case 3
prompt = {'請輸入管路流量(m^3/s)[10]','請輸入入口管徑(m)[1]:','請輸入出口管徑(m)[2]:'};
dlg_title = '您所選擇的是擴大管';
num_lines = 1;
def = {'10','1','2'};
answer = inputdlg(prompt,dlg_title,num_lines,def);
Q=answer{1,1};d1=answer{2,1};d2=answer{3,1};
ke=Q./(pi*d1.^2/4)/(2*9.81);
HL=(1-(d1./d2).^2).*ke;
end
figure('Position',[400 400 400 300],'Name','結果')
uicontrol('style','text','position',[160 200 80 80],'string','此接頭損失為')
uicontrol('style','text','position',[100 90 200 100],'string',HL)
result=questdlg('是否繼續執行?','程式執行詢問','Yes','No','No');
if strcmp(result,'No');
break
end
end
或是點此
網頁
plot作圖時
如果新的plot圖時,會將前一次的洗掉,做出第二次的繪圖,舉例如下
第一次plot作圖如果這時候在使用plot繪製另一個圖形的話,前一次的作圖就會消失
第二次plot作圖若是要兩個圖顯示在一個figure的話,則必須用hold on指令
以hold on將兩張圖合併如果要繪製三度空間的圖形的話,則必須要使用plot3的指令
plot3作圖line作圖
若是以line的指令作圖時,連續使用line繪製不同函數時,則可以不必使用hold on的指令,即可繪製在同一個figure
以line繪製兩個函數雖然說line可以給予三個變數繪製三度空間的圖,但是實際上使用後會發現繪製仍為2D平面的圖,並且是前面兩個變數的圖型
plot繪製三度空間圖此時如果要會製成三度空間圖的話,則可以用plot3先繪製一點或是一個三度空間圖形
以plot3繪製三度空間點最後在重新輸入line的函數,即可再三度空間繪圖
line指令三度空間繪圖

















